Lintas Pengetahuan

Kembali lagi Lintas Pengetahuan Terkini menghadirkan artikel artikel Pengetahuan -pengetahuan tenteng dunia Pengetahuan Fisika dan pengetahuan dasar lainnya. kali ini Lintas Pengetahuan Terkini  menghadirkan artikel tentang Gelombang Berjalan.
langsung aja gan bisa dibaca artikel dibawah ini. ^-^

Gelombang berjalan yang akan dibahas di sini adalahPersamaan Gelombang Berjalan dan Sudut Fase, Fase, dan Beda Fase pada Gelombang Berjalan. Sebelumnya pada pembahasan Fisika SMA Kelas 12 kita sudah membahas pada pokok pembahasan Gelombang yaitu Jenis Gelombang dan Sifatnya.

1. Persamaan Gelombang Berjalan 

Seutas tali AB yang kita bentangkan mendatar perhatikan gambar di bawah. Ujung B diikatkan pada tiang, sedangkan ujung A kita pegang. Apabila ujung A kita getarkan naik turun terusmenerus, maka pada tali tersebut akan terjadi rambatan gelombang dari ujung A ke ujung B. Misalkan amplitudo getarannya A dan gelombang merambat dengan kecepatan v dan periode getarannya T.

Misalkan titik P terletak pada tali AB berjarak x dari ujung A dan apabila titik A telah bergetar selama t sekon, maka titik P telah bergetar selama  , di mana 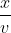 adalah waktu yang diperlukan gelombang merambat dari A ke P.

Persamaan simpangan titik P pada saat itu dapat dinyatakan sebagai berikut :

di mana 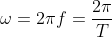 maka persamaan tersebut dapat ditulis menjadi :

Jika , di mana k didefinisikan sebagai bilangan gelombang maka persamaan simpangan dapat dituliskan menjadi :

Persamaan tersebut yang disebut sebagai persamaan gelombang berjalan yang secara umum dapat dituliskan :

Dalam persamaan di atas dipakai nilai negatif (-) jika gelombang berasal dari sebelah kiri titik P atau gelombang merambat ke kanan dan dipakai positif (+) jika gelombang berasal dari sebelah kanan titik P atau gelombang merambat ke kiri.

2. Sudut Fase, Fase, dan Beda Fase pada Gelombang 

Seperti halnya pada getaran, pada gelombang pun dikenal pengertian sudut fase, fase, dan beda fase. Oleh karena itu perhatikan lagi persamaan gelombang berjalan berikut ini!

di mana   disebut sudut fase sehingga :

Mengingat hubungan antara sudut fase () dengan fase () adalah 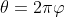 maka fase titik P adalah:

Apabila pada tali tersebut terdapat dua buah titik, titik P yang berjarak 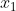 dari titik asal getaran dan titik Q yang berjarak  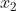 dari titik asal getaran, maka besarnya beda fase antara titik P dan Q adalah

 Jangan cuma dibaca aja gan comen juga ya (y)